What is the K-Nearest Neighbors Algorithm?

KNN (K-Nearest Neighbors) is one of the simplest yet most important classification algorithms in machine learning. It falls under the category of supervised learning and is widely used in areas like pattern recognition, data mining, and intrusion detection. The algorithm works by using a set of prior data (called training data), which groups different coordinates based on a certain attribute.

For example, consider a table of data points with two features:

Visualization of KNN Algorithm 

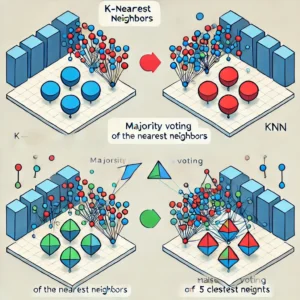
Here is a visualization of the K-Nearest Neighbors (KNN) algorithm. The data points are represented by two different shapes or colors, with lines connecting a new point to its nearest neighbors, illustrating the classification process based on majority voting.

Why do we need a KNN algorithm?

he K-Nearest Neighbors (K-NN) algorithm is a flexible and widely used machine learning method known for its simplicity and ease of implementation. Unlike some other algorithms, it doesn’t make any assumptions about the data distribution and can handle both numerical and categorical data, making it suitable for a variety of datasets in both classification and regression tasks. Being a non-parametric algorithm, K-NN makes predictions by analyzing the similarity between data points without relying on any specific model or distribution.

Key Features of K-NN:

• Non-parametric: It doesn’t assume any form for the underlying data.
• Versatility: It can be used for both classification (categorizing data) and regression (predicting continuous values).
• Robust to Outliers: It is less sensitive to outliers compared to many other machine learning algorithms.

How K-NN Works:

K-NN finds the K nearest neighbors to a data point based on a distance metric (e.g., Euclidean distance). The prediction for the data point is then determined by either:

• Majority vote (for classification): The class that appears most frequently among the K neighbors is assigned to the new data point.
• Averaging (for regression): The value is predicted as the average of the K nearest data points.

This local approach allows the algorithm to adapt well to different patterns and structures in the dataset.

Distance Metrics Used in K-NN:

To find the nearest neighbors, the K-NN algorithm uses distance metrics. These metrics help identify which points or groups are closest to the query point. Some common distance metrics include:

1. Euclidean Distance: The straight-line distance between two points in a multidimensional space.
2. Manhattan Distance: The sum of the absolute differences between the coordinates of two points.
3. Minkowski Distance: A generalization of both Euclidean and Manhattan distances.
4. Hamming Distance: Used for categorical variables, it measures the difference between two strings of equal length.
5. Cosine Similarity: Measures the cosine of the angle between two vectors, often used in text classification.

These metrics allow K-NN to adapt to different types of data and problem domains effectively. Would you like to explore a specific distance metric or need further details on any of these?

.

How to choose the value of k for KNN Algorithm?

he value of K is a critical parameter in the K-Nearest Neighbors (K-NN) algorithm, as it determines how many neighbors will be considered when making predictions. Choosing the right value of K is essential to the performance and accuracy of the algorithm. Here are some important considerations when selecting K:

1. Effect of K on Bias-Variance Tradeoff:

• Low K values (e.g., K = 1):
  • The model will be more sensitive to noise and outliers.
  • This can lead to overfitting, where the algorithm captures noise rather than the underlying pattern.
• High K values (e.g., K = 10 or more):
  • The algorithm becomes more generalized, as it considers more neighbors, which reduces the impact of any single noisy point.
  • This can lead to underfitting, where the model is too simplistic and may miss important patterns in the data.

2. Choosing the Right K:

• Data Characteristics: The value of K should reflect the nature of the data:
  • If the data has more noise or outliers, a higher K value is generally preferred to smooth out anomalies.
  • For cleaner datasets with fewer outliers, a lower K value may work better, capturing local details more accurately.
• Odd vs. Even K: It’s often recommended to choose an odd value for K in classification tasks. This avoids ties, especially in binary classification where an even K might result in equal votes between two classes.

3. Impact on Classification:

• When K = 1, the algorithm is highly sensitive to the nearest neighbor, potentially making it very accurate on the training data but less robust on test data.
• With higher K values, the algorithm averages out the decisions of multiple neighbors, which can improve stability and reduce the impact of outliers but may miss fine details in the data.

4. Techniques to Choose K:

• Cross-validation: One common approach is to use cross-validation to test various values of K and find the one that provides the best performance.
• Elbow method: Another method is to plot the error rate for different values of K and look for an “elbow point” where the error starts to flatten. This can indicate a good balance between bias and variance.

In summary, choosing the right K involves balancing the sensitivity to noise (lower K) and generalization ability (higher K), and it’s important to experiment with different values based on the data at hand. Would you like to explore techniques for tuning K further or need assistance with a specific dataset?

 

Workings of KNN algorithm

Thе K-Nearest Neighbors (KNN) algorithm operates on the principle of similarity, where it predicts the label or value of a new data point by considering the labels or values of its K nearest neighbors in the training dataset.

Step-by-Step explanation of how KNN works is discussed below:

Step 1: Selecting the optimal value of K

• K represents the number of nearest neighbors that needs to be considered while making prediction.

Step 2: Calculating distance

• To measure the similarity between target and training data points, Euclidean distance is used. Distance is calculated between each of the data points in the dataset and target point.

Step 3: Finding Nearest Neighbors

• The k data points with the smallest distances to the target point are the nearest neighbors.

Step 4: Voting for Classification or Taking Average for Regression

• In the classification problem, the class labels of K-nearest neighbors are determined by performing majority voting. The class with the most occurrences among the neighbors becomes the predicted class for the target data point.
• In the regression problem, the class label is calculated by taking average of the target values of K nearest neighbors. The calculated average value becomes the predicted output for the target data point.